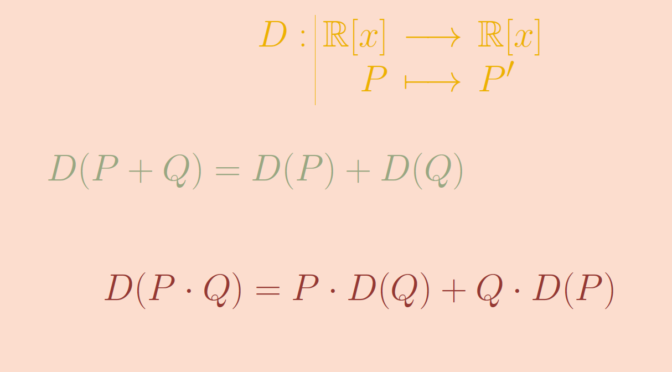A ring homomorphism is a function between two rings which respects the structure. Let’s provide examples of functions between rings which respect the addition or the multiplication but not both.

An additive group homomorphism that is not a ring homomorphism

We consider the ring \(\mathbb R[x]\) of real polynomials and the derivation \[
\begin{array}{l|rcl}
D : & \mathbb R[x] & \longrightarrow & \mathbb R[x] \\
& P & \longmapsto & P^\prime \end{array}\] \(D\) is an additive homomorphism as for all \(P,Q \in \mathbb R[x]\) we have \(D(P+Q) = D(P) + D(Q)\). However, \(D\) does not respect the multiplication as \[
D(x^2) = 2x \neq 1 = D(x) \cdot D(x).\] More generally, \(D\) satisfies the Leibniz rule \[
D(P \cdot Q) = P \cdot D(Q) + Q \cdot D(P).\]

A multiplication group homomorphism that is not a ring homomorphism

The function \[
\begin{array}{l|rcl}
f : & \mathbb R & \longrightarrow & \mathbb R \\
& x & \longmapsto & x^2 \end{array}\] is a multiplicative group homomorphism of the group \((\mathbb R, \cdot)\). However \(f\) does not respect the addition.