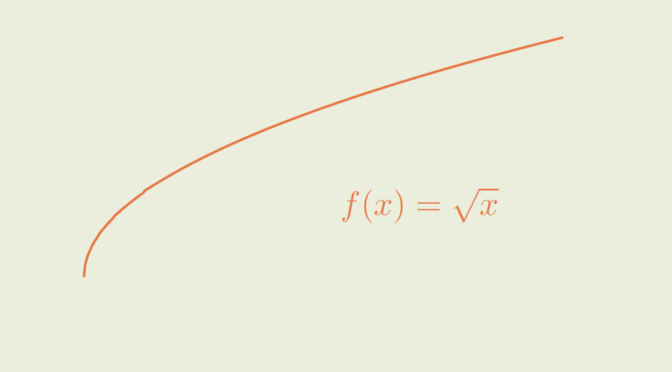Consider the function \[
\begin{array}{l|rcl}
f : & [0,1] & \longrightarrow & [0,1] \\
& x & \longmapsto & \sqrt{x} \end{array}\]

\(f\) is continuous on the compact interval \([0,1]\). Hence \(f\) is uniform continuous on that interval according to Heine-Cantor theorem. For a direct proof, one can verify that for \(\epsilon > 0\), one have \(\vert \sqrt{x} – \sqrt{y} \vert \le \epsilon\) for \(\vert x – y \vert \le \epsilon^2\).

However \(f\) is not Lipschitz continuous. If \(f\) was Lipschitz continuous for a Lipschitz constant \(K > 0\), we would have \(\vert \sqrt{x} – \sqrt{y} \vert \le K \vert x – y \vert\) for all \(x,y \in [0,1]\). But we get a contradiction taking \(x=0\) and \(y=\frac{1}{4 K^2}\) as \[
\vert \sqrt{x} – \sqrt{y} \vert = \frac{1}{2 K} > \frac{1}{4 K} = K \vert x – y \vert\]