Let \(f_1(x) = |x|\) for \(| x | \le \frac{1}{2}\), and let \(f_1\) be defined for other values of \(x\) by periodic continuation with period \(1\). \(f_1\) graph looks like following picture:
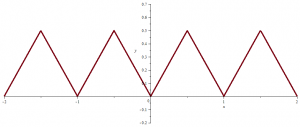
\(f_1\) is continuous everywhere and differentiable on \(\mathbb{R} \setminus \mathbb{Z}\).
For \(n > 1\) define \(f_n(x)=\frac{f_1(4^{n-1} x)}{4^{n-1}}\), so that for every positive integer \(n\), \(f_n\) is a continuous periodic function of period \(\frac{1}{4^{n-1}}\) and maximum value \(\frac{1}{2 \cdot 4^{n-1}}\).
Finally, define \(f\) for \(x \in \mathbb{R}\) by:
\[f(x) = \sum_{n=1}^{+ \infty} f_n(x) = \sum_{n=1}^{+ \infty} \frac{f_1(4^{n-1} x)}{4^{n-1}}\]
The function series \((f_n)_{n \ge 1}\) is normally convergent and therefore \(f\) is continuous.
\(f\) is nowhere differentiable
To see this let \(a\) be an arbitrary real number.
For any positive integer \(n\), choose \(h_n\) to be either \(\frac{1}{4^n}\) or \(-\frac{1}{4^n}\) so that \(|f_n(a+h_n)-f_n(a)|=|h_n|\). This is possible because \(h_n\) is equal to a quarter of the period of \(f_n\) while \(f_n\) is a linear function of slope \(\pm 1\) in an interval of length \(2 h_n\) containing \(a\).
\(|f_m(a+h_n)-f_m(a)|\) has this same value \(|h_n|\) for all \(m \le n\), and vanishes for \(m > n\). Hence the difference quotient \(\frac{f(a+h_n)-f(a)}{h_n}\) is an integer whose parity is the one of \(n\). It follows that:
\[\lim\limits_{n \to \infty} \frac{f(a+h_n)-f(a)}{h_n}\] cannot exist, which proves that \(f\) is not differentiable at point \(a\) which was arbitrarily chosen.
\(f\) is also nowhere monotonic
For any point of the form \(a=\frac{k}{4^m}\), where \(k\) is an integer and \(m\) a positive integer, we have \(f_n(a)=0\) for \(n > m\) and hence
\[f(a)=\sum_{i=1}^m f_i(a)\] Let \(h_m=\frac{1}{4^{2m+1}}\), \(h_m\) is a period of \(f_n\) for \(n > 2m+1\) and therefore \(f_n(a+h_m)=0\). Hence \[
\begin{aligned}
f(a+h_m)-f(a) &= \sum_{n=1}^m (f_n(a+h_m)-f_n(a)) + \sum_{n=m+1}^{2m+1} f_n(a+h_m)\\
&\ge -m h_m + (m+1)h_m >0
\end{aligned}\] Similarly \(f(a-h_m)-f(a) \ge h_m > 0\). As numbers of the form \(\frac{k}{4^m}\) are dense, \(f\) cannot be monotonic in no open interval.
The first example of a continuous real function nowhere differentiable was shown by Karl Weierstrass in 1872. See Wikipedia – Weierstrass function for more details.

