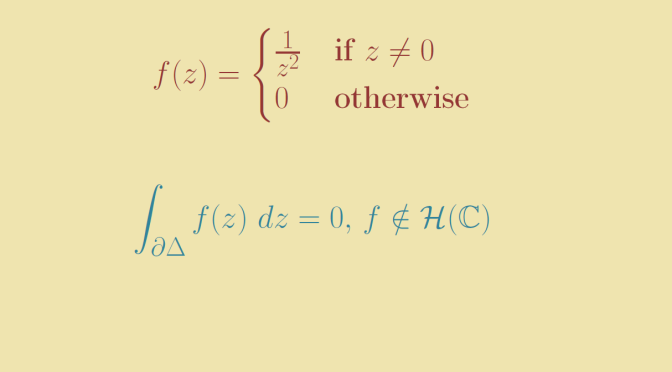Let’s recall Morera’s theorem.
Morera’s theorem Suppose that \(f\) is a continuous complex-valued function in a connected open set \(\Omega \subset \mathbb C\) such that
\[\int_{\partial \Delta} f(z) \ dz = 0\] for every closed triangle \(\Delta \subset \Omega \setminus \{p\}\) where \(p \in \Omega\). Then \(f\) is holomorphic in \(\Omega\).
Does the conclusion of Morera’s theorem still hold if \(f\) is supposed to be continuous only in \(\Omega \setminus \{p\}\)? The answer is negative and we provide a counterexample.
Let \(\Omega\) be the entire complex plane, \(f\) defined as follows
\[f(z)=\begin{cases}
\frac{1}{z^2} & \text{if } z \neq 0\\
0 & \text{otherwise}
\end{cases}\] and \(p\) the origin.
For \(a,b \in \Omega \setminus \{0\}\) we have
\[\begin{aligned}
\int_{[a,b]} f(z) \ dz &= \int_{[a,b]} \frac{dz}{z^2}\\
&= \int_0^1 \frac{b-a}{[a+t(b-a)]^2} \ dt\\
&=\left[ -\frac{1}{a+t(b-a)} \right]_0^1 = \frac{1}{a} – \frac{1}{b}
\end{aligned}\]
Hence for a triangle \(\Delta\) with vertices at \(a,b ,c \in \Omega \setminus \{0\}\):
\[\int_{\partial \Delta} f(z) \ dz = \left( \frac{1}{a} – \frac{1}{b} \right) + \left( \frac{1}{b} – \frac{1}{c} \right) + \left( \frac{1}{c} – \frac{1}{a} \right)=0\]
However, \(f\) is not holomorphic in \(\Omega\) as it is even not continuous at \(0\).