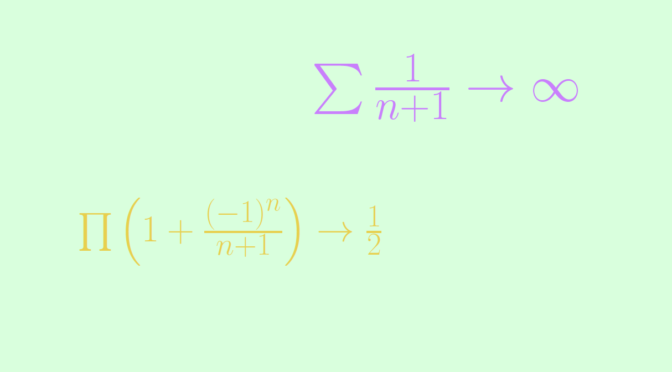Let’s recall two theorems about infinite products \(\prod \ (1+a_n)\). The first one deals with nonnegative terms \(a_n\).

THEOREM 1 An infinite product \(\prod \ (1+a_n)\) with nonnegative terms \(a_n\) converges if and only if the series \(\sum a_n\) converges.

The second is related to infinite products with complex terms.

THEOREM 2 The absolute convergence of the series \(\sum a_n\) implies the convergence of the infinite product \(\prod \ (1+a_n)\). Moreover \(\prod \ (1+a_n)\) is not zero providing \(a_n \neq -1\) for all \(n \in \mathbb N\).

The converse of Theorem 2 is not true as shown by following counterexample.

We consider \(a_n=(-1)^n/(n+1)\). For \(N \in \mathbb N\) we have:
\[\prod_{n=1}^N \ (1+a_n) =
\begin{cases}
\frac{1}{2} &\text{ for } N \text{ odd}\\
\frac{1}{2}(1+\frac{1}{N+1}) &\text{ for } N \text{ even}
\end{cases}
\] hence the infinite product \(\prod \ (1+a_n)\) converges (to \(\frac{1}{2}\)) while the series \(\sum \left\vert a_n \right\vert = \sum \frac{1}{n+1}\) diverges (it is the harmonic series with first term omitted).