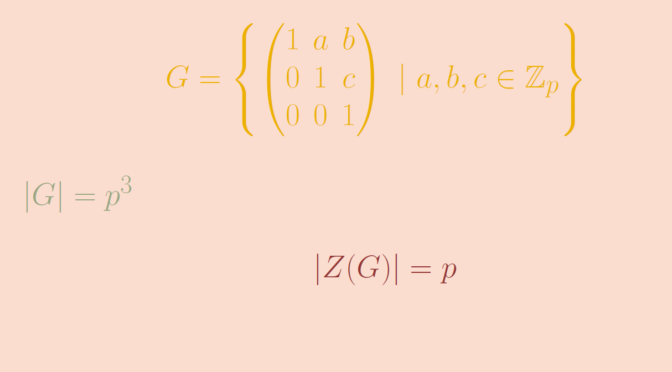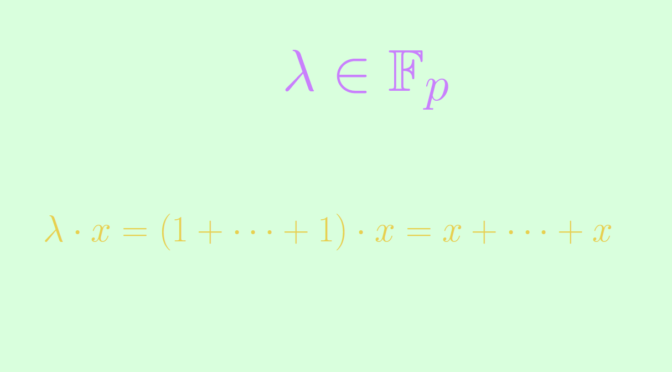Category Archives: Algebra

Algebra

A nonabelian \(p\)-group

Leave a comment

Consider a prime number \(p\) and a finite p-group \(G\), i.e. a group of order \(p^n\) with \(n \ge 1\).

If \(n=1\) the group \(G\) is cyclic hence abelian.

For \(n=2\), \(G\) is also abelian. This is a consequence of the fact that the center \(Z(G)\) of a \(p\)-group is non-trivial. Indeed if \(\vert Z(G) \vert =p^2\) then \(G=Z(G)\) is abelian. We can’t have \(\vert Z(G) \vert =p\). If that would be the case, the order of \(H=G / Z(G) \) would be equal to \(p\) and \(H\) would be cyclic, generated by an element \(h\). For any two elements \(g_1,g_2 \in G\), we would be able to write \(g_1=h^{n_1} z_1\) and \(g_2=h^{n_1} z_1\) with \(z_1,z_2 \in Z(G)\). Hence \[
g_1 g_2 = h^{n_1} z_1 h^{n_2} z_2=h^{n_1 + n_2} z_1 z_2= h^{n_2} z_2 h^{n_1} z_1=g_2 g_1,\] proving that \(g_1,g_2\) commutes in contradiction with \(\vert Z(G) \vert < \vert G \vert\). However, all \(p\)-groups are not abelian. For example the unitriangular matrix group \[
U(3,\mathbb Z_p) = \left\{
\begin{pmatrix}
1 & a & b\\
0 & 1 & c\\
0 & 0 & 1\end{pmatrix} \ | \ a,b ,c \in \mathbb Z_p \right\}\] is a \(p\)-group of order \(p^3\). Its center \(Z(U(3,\mathbb Z_p))\) is \[
Z(U(3,\mathbb Z_p)) = \left\{
\begin{pmatrix}
1 & 0 & b\\
0 & 1 & 0\\
0 & 0 & 1\end{pmatrix} \ | \ b \in \mathbb Z_p \right\},\] which is of order \(p\). Therefore \(U(3,\mathbb Z_p)\) is not abelian.

Algebra

Subset of elements of finite order of a group

Leave a comment

Consider a group \(G\) and have a look at the question: is the subset \(S\) of elements of finite order a subgroup of \(G\)?

The answer is positive when any two elements of \(S\) commute. For the proof, consider \(x,y \in S\) of order \(m,n\) respectively. Then \[
\left(xy\right)^{mn} = x^{mn} y^{mn} = (x^m)^n (y^n)^m = e\] where \(e\) is the identity element. Hence \(xy\) is of finite order (less or equal to \(mn\)) and belong to \(S\).

Example of a non abelian group

In that cas, \(S\) might not be subgroup of \(G\). Let’s take for \(G\) the general linear group over \(\mathbb Q\) (the set of rational numbers) of \(2 \times 2\) invertible matrices named \(\text{GL}_2(\mathbb Q)\). The matrices \[
A = \begin{pmatrix}0&1\\1&0\end{pmatrix},\ B=\begin{pmatrix}0 & 2\\\frac{1}{2}& 0\end{pmatrix}\] are of order \(2\). They don’t commute as \[
AB = \begin{pmatrix}\frac{1}{2}&0\\0&2\end{pmatrix} \neq \begin{pmatrix}2&0\\0&\frac{1}{2}\end{pmatrix}=BA.\] Finally, \(AB\) is of infinite order and therefore doesn’t belong to \(S\) proving that \(S\) is not a subgroup of \(G\).

Algebra

Field not algebraic over an intersection but algebraic over each initial field

Leave a comment

Let’s describe an example of a field \(K\) which is of degree \(2\) over two distinct subfields \(M\) and \(N\) respectively, but not algebraic over \(M \cap N\).

Let \(K=F(x)\) be the rational function field over a field \(F\) of characteristic \(0\), \(M=F(x^2)\) and \(N=F(x^2+x)\). I claim that those fields provide the example we’re looking for.

\(K\) is of degree \(2\) over \(M\) and \(N\)

The polynomial \(\mu_M(t)=t^2-x^2\) belongs to \(M[t]\) and \(x \in K\) is a root of \(\mu_M\). Also, \(\mu_M\) is irreducible over \(M=F(x^2)\). If that wasn’t the case, \(\mu_M\) would have a root in \(F(x^2)\) and there would exist two polynomials \(p,q \in F[t]\) such that \[
p^2(x^2) = x^2 q^2(x^2)\] which cannot be, as can be seen considering the degrees of the polynomials of left and right hand sides. This proves that \([K:M]=2\). Considering the polynomial \(\mu_N(t)=t^2-t-(x^2+x)\), one can prove that we also have \([K:N]=2\).

We have \(M \cap N=F\)

The mapping \(\sigma_M : x \mapsto -x\) extends uniquely to an \(F\)-automorphism of \(K\) and the elements of \(M\) are fixed under \(\sigma_M\). Similarly, the mapping \(\sigma_N : x \mapsto -x-1\) extends uniquely to an \(F\)-automorphism of \(K\) and the elements of \(N\) are fixed under \(\sigma_N\). Also \[
(\sigma_N\circ\sigma_M)(x)=\sigma_N(\sigma_M(x))=\sigma_N(-x)=-(-x-1)=x+1.\] An element \(z=p(x)/q(x) \in M \cap N\) where \(p(x),q(x)\) are coprime polynomials of \(K=F(x)\) is fixed under \(\sigma_M \circ \sigma_N\). Therefore following equality holds \[
\frac{p(x)}{q(x)}=z=(\sigma_2\circ\sigma_1)(z)=\frac{p(x+1)}{q(x+1)},\] which is equivalent to \[
p(x)q(x+1)=p(x+1)q(x).\] By induction, we get for \(n \in \mathbb Z\) \[
p(x)q(x+n)=p(x+n)q(x).\] Assume \(p(x)\) is not a constant polynomial. Then it has a root \(\alpha\) in some finite extension \(E\) of \(F\). As \(p(x),q(x)\) are coprime polynomials, \(q(\alpha) \neq 0\). Consequently \(p(\alpha+n)=0\) for all \(n \in \mathbb Z\) and the elements \(\alpha +n\) are all distinct as the characteristic of \(F\) is supposed to be non zero. This implies that \(p(x)\) is the zero polynomial, in contradiction with our assumption. Therefore \(p(x)\) is a constant polynomial and \(q(x)\) also according to a similar proof. Hence \(z\) is constant as was supposed to be proven.

Finally, \(K=F(x)\) is not algebraic over \(F=M \cap N\) as \((1,x, x^2, \dots, x^n, \dots)\) is independent over the field \(F\) which concludes our claims on \(K, M\) and \(N\).

Algebra

Complex matrix without a square root

Leave a comment

Consider for \(n \ge 2\) the linear space \(\mathcal M_n(\mathbb C)\) of complex matrices of dimension \(n \times n\). Is a matrix \(T \in \mathcal M_n(\mathbb C)\) always having a square root \(S \in \mathcal M_n(\mathbb C)\), i.e. a matrix such that \(S^2=T\)? is the question we deal with.

First, one can note that if \(T\) is similar to \(V\) with \(T = P^{-1} V P\) and \(V\) has a square root \(U\) then \(T\) also has a square root as \(V=U^2\) implies \(T=\left(P^{-1} U P\right)^2\).

Diagonalizable matrices

Suppose that \(T\) is similar to a diagonal matrix \[
D=\begin{bmatrix}
d_1 & 0 & \dots & 0 \\
0 & d_2 & \dots & 0 \\
\vdots & \vdots & \ddots & 0 \\
0 & 0 & \dots & d_n
\end{bmatrix}\] Any complex number has two square roots, except \(0\) which has only one. Therefore, each \(d_i\) has at least one square root \(d_i^\prime\) and the matrix \[
D^\prime=\begin{bmatrix}
d_1^\prime & 0 & \dots & 0 \\
0 & d_2^\prime & \dots & 0 \\
\vdots & \vdots & \ddots & 0 \\
0 & 0 & \dots & d_n^\prime
\end{bmatrix}\] is a square root of \(D\). Continue reading Complex matrix without a square root →

Algebra

Additive subgroups of vector spaces

Leave a comment

Consider a vector space \(V\) over a field \(F\). A subspace \(W \subseteq V\) is an additive subgroup of \((V,+)\). The converse might not be true.

If the characteristic of the field is zero, then a subgroup \(W\) of \(V\) might not be an additive subgroup. For example \(\mathbb R\) is a vector space over \(\mathbb R\) itself. \(\mathbb Q\) is an additive subgroup of \(\mathbb R\). However \(\sqrt{2}= \sqrt{2}.1 \notin \mathbb Q\) proving that \(\mathbb Q\) is not a subspace of \(\mathbb R\).

Another example is \(\mathbb Q\) which is a vector space over itself. \(\mathbb Z\) is an additive subgroup of \(\mathbb Q\), which is not a subspace as \(\frac{1}{2} \notin \mathbb Z\).

Yet, an additive subgroup of a vector space over a prime field \(\mathbb F_p\) with \(p\) prime is a subspace. To prove it, consider an additive subgroup \(W\) of \((V,+)\) and \(x \in W\). For \(\lambda \in F\), we can write \(\lambda = \underbrace{1 + \dots + 1}_{\lambda \text{ times}}\). Consequently \[
\lambda \cdot x = (1 + \dots + 1) \cdot x= \underbrace{x + \dots + x}_{\lambda \text{ times}} \in W.\]

Finally an additive subgroup of a vector space over any finite field is not always a subspace. For a counterexample, take the non-prime finite field \(\mathbb F_{p^2}\) (also named \(\text{GF}(p^2)\)). \(\mathbb F_{p^2}\) is also a vector space over itself. The prime finite field \(\mathbb F_p \subset \mathbb F_{p^2}\) is an additive subgroup that is not a subspace of \(\mathbb F_{p^2}\).

Algebra

Non commutative rings

Leave a comment

Let’s recall that a set \(R\) equipped with two operations \((R,+,\cdot)\) is a ring if and only if \((R,+)\) is an abelian group, multiplication \(\cdot\) is associative and has a multiplicative identity \(1\) and multiplication is left and right distributive with respect to addition.

\((\mathbb Z, +, \cdot)\) is a well known infinite ring which is commutative. The rational, real and complex numbers are other infinite commutative rings. Those are in fact fields as every non-zero element have a multiplicative inverse.

For a field \(F\) (finite or infinite), the polynomial ring \(F[X]\) is another example of infinite commutative ring.

Also for \(n\) integer, the integers modulo n is a finite ring that is commutative. Finally, according to Wedderburn theorem every finite division ring is commutative.

So what are examples of non commutative rings? Let’s provide a couple. Continue reading Non commutative rings →

Algebra

A linear map without any minimal polynomial

Leave a comment

Given an endomorphism \(T\) on a finite-dimensional vector space \(V\) over a field \(\mathbb F\), the minimal polynomial \(\mu_T\) of \(T\) is well defined as the generator (unique up to units in \(\mathbb F\)) of the ideal:\[
I_T= \{p \in \mathbb F[t]\ ; \ p(T)=0\}.\]

For infinite-dimensional vector spaces, the minimal polynomial might not be defined. Let’s provide an example.

We take the real polynomials \(V = \mathbb R [t]\) as a real vector space and consider the derivative map \(D : P \mapsto P^\prime\). Let’s prove that \(D\) doesn’t have any minimal polynomial. By contradiction, suppose that \[
\mu_D(t) = a_0 + a_1 t + \dots + a_n t^n \text{ with } a_n \neq 0\] is the minimal polynomial of \(D\), which means that for all \(P \in \mathbb R[t]\) we have \[
a_0 + a_1 P^\prime + \dots + a_n P^{(n)} = 0.\] Taking for \(P\) the polynomial \(t^n\) we get \[
a_0 t^n + n a_1 t^{n-1} + \dots + n! a_n = 0,\] which doesn’t make sense as \(n! a_n \neq 0\), hence \(a_0 t^n + n a_1 t^{n-1} + \dots + n! a_n\) cannot be the zero polynomial.

We conclude that \(D\) doesn’t have any minimal polynomial.

Algebra

Non linear map preserving Euclidean norm

Leave a comment

Let \(V\) be a real vector space endowed with an Euclidean norm \(\Vert \cdot \Vert\).

A bijective map \( T : V \to V\) that preserves inner product \(\langle \cdot, \cdot \rangle\) is linear. Also, Mazur-Ulam theorem states that an onto map \( T : V \to V\) which is an isometry (\( \Vert T(x)-T(y) \Vert = \Vert x-y \Vert \) for all \(x,y \in V\)) and fixes the origin (\(T(0) = 0\)) is linear.

What about an application that preserves the norm (\(\Vert T(x) \Vert = \Vert x \Vert\) for all \(x \in V\))? \(T\) might not be linear as we show with following example:\[
\begin{array}{l|rcll}
T : & V & \longrightarrow & V \\
& x & \longmapsto & x & \text{if } \Vert x \Vert \neq 1\\
& x & \longmapsto & -x & \text{if } \Vert x \Vert = 1\end{array}\]

It is clear that \(T\) preserves the norm. However \(T\) is not linear as soon as \(V\) is not the zero vector space. In that case, consider \(x_0\) such that \(\Vert x_0 \Vert = 1\). We have:\[
\begin{cases}
T(2 x_0) &= 2 x_0 \text{ as } \Vert 2 x_0 \Vert = 2\\
\text{while}\\
T(x_0) + T(x_0) = -x_0 + (-x_0) &= – 2 x_0
\end{cases}\]

Algebra

Non linear map preserving orthogonality

Leave a comment

Let \(V\) be a real vector space endowed with an inner product \(\langle \cdot, \cdot \rangle\).

It is known that a bijective map \( T : V \to V\) that preserves the inner product \(\langle \cdot, \cdot \rangle\) is linear.

That might not be the case if \(T\) is supposed to only preserve orthogonality. Let’s consider for \(V\) the real plane \(\mathbb R^2\) and the map \[
\begin{array}{l|rcll}
T : & \mathbb R^2 & \longrightarrow & \mathbb R^2 \\
& (x,y) & \longmapsto & (x,y) & \text{for } xy \neq 0\\
& (x,0) & \longmapsto & (0,x)\\
& (0,y) & \longmapsto & (y,0) \end{array}\]

The restriction of \(T\) to the plane less the x-axis and the y-axis is the identity and therefore is bijective on this set. Moreover \(T\) is a bijection from the x-axis onto the y-axis, and a bijection from the y-axis onto the x-axis. This proves that \(T\) is bijective on the real plane.

\(T\) preserves the orthogonality on the plane less x-axis and y-axis as it is the identity there. As \(T\) swaps the x-axis and the y-axis, it also preserves orthogonality of the coordinate axes. However, \(T\) is not linear as for non zero \(x \neq y\) we have: \[
\begin{cases}
T[(x,0) + (0,y)] = T[(x,y)] &= (x,y)\\
\text{while}\\
T[(x,0)] + T[(0,y)] = (0,x) + (y,0) &= (y,x)
\end{cases}\]

Algebra

A linear map having all numbers as eigenvalue

Leave a comment

Consider a linear map \(\varphi : E \to E\) where \(E\) is a linear space over the field \(\mathbb C\) of the complex numbers. When \(E\) is a finite dimensional vector space of dimension \(n \ge 1\), the number of eigenvalues is finite. The eigenvalues are the roots of the characteristic polynomial \(\chi_\varphi\) of \(\varphi\). \(\chi_\varphi\) is a complex polynomial of degree \(n \ge 1\). Therefore the set of eigenvalues of \(\varphi\) is non-empty and its cardinal is less than \(n\).

Things are different when \(E\) is an infinite dimensional space.

A linear map having all numbers as eigenvalue

Let’s consider the linear space \(E=\mathcal C^\infty([0,1])\) of smooth complex functions having derivatives of all orders and defined on the segment \([0,1]\). \(E\) is an infinite dimensional space: it contains all the polynomial maps.

On \(E\), we define the linear map \[\begin{array}{l|rcl}
\varphi : & \mathcal C^\infty([0,1]) & \longrightarrow & \mathcal C^\infty([0,1]) \\
& f & \longmapsto & f^\prime \end{array}\]

The set of eigenvalues of \(\varphi\) is all \(\mathbb C\). Indeed, for \(\lambda \in \mathbb C\) the map \(t \mapsto e^{\lambda t}\) is an eigenvector associated to the eigenvalue \(\lambda\).

A linear map having no eigenvalue

On the same linear space \(E=\mathcal C^\infty([0,1])\), we now consider the linear map \[\begin{array}{l|rcl}
\psi : & \mathcal C^\infty([0,1]) & \longrightarrow & \mathcal C^\infty([0,1]) \\
& f & \longmapsto & x f \end{array}\]

Suppose that \(\lambda \in \mathbb C\) is an eigenvalue of \(\psi\) and \(h \in E\) an eigenvector associated to \(\lambda\). By hypothesis, there exists \(x_0 \in [0,1]\) such that \(h(x_0) \neq 0\). Even better, as \(h\) is continuous, \(h\) is non-vanishing on \(J \cap [0,1]\) where \(J\) is an open interval containing \(x_0\). On \(J \cap [0,1]\) we have the equality \[
(\psi(h))(x) = x h(x) = \lambda h(x)\] Hence \(x=\lambda\) for all \(x \in J \cap [0,1]\). A contradiction proving that \(\psi\) has no eigenvalue.