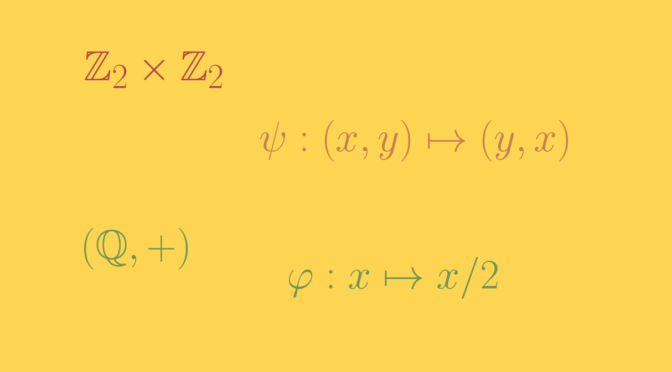Let’s \(G\) be a group. A characteristic subgroup is a subgroup \(H \subseteq G\) that is mapped to itself by every automorphism of \(G\).
An inner automorphism is an automorphism \(\varphi \in \mathrm{Aut}(G)\) defined by a formula \(\varphi : x \mapsto a^{-1}xa\) where \(a\) is an element of \(G\). An automorphism of a group which is not inner is called an outer automorphism. And a subgroup \(H \subseteq G\) that is mapped to itself by every inner automorphism of \(G\) is called a normal subgroup.
Obviously a characteristic subgroup is a normal subgroup. The converse is not true as we’ll see below.
Example of a direct product
Let \(K\) be a nontrivial group. Then consider the group \(G = K \times K\). The subgroups \(K_1=\{e\} \times K\) and \(K_2=K \times \{e\} \) are both normal in \(G\) as for \((e, k) \in K_1\) and \((a,b) \in G\) we have
\[(a,b)^{-1} (e,x) (a,b) = (a^{-1},b^{-1}) (e,x) (a,b) = (e,b^{-1}xb) \in K_1\] and \(b^{-1}K_1 b = K_1\). Similar relations hold for \(K_2\). As \(K\) is supposed to be nontrivial, we have \(K_1 \neq K_2\).
The exchange automorphism \(\psi : (x,y) \mapsto (y,x)\) exchanges the subgroup \(K_1\) and \(K_2\). Thus, neither \(K_1\) nor \(K_2\) is invariant under all the automorphisms, so neither is characteristic. Therefore, \(K_1\) and \(K_2\) are both normal subgroups of \(G\) that are not characteristic.
When \(K = \mathbb Z_2\) is the cyclic group of order two, \(G = \mathbb Z_2 \times \mathbb Z_2\) is the Klein four-group. In particular, this gives a counterexample where the ambient group is an abelian group.
Example on the additive group \(\mathbb Q\)
Consider the additive group \((\mathbb Q,+)\) of rational numbers. The map \(\varphi : x \mapsto x/2\) is an automorphism. As \((\mathbb Q,+)\) is abelian, all subgroups are normal. However, the subgroup \(\mathbb Z\) is not sent into itself by \(\varphi\) as \(\varphi(1) = 1/ 2 \notin \mathbb Z\). Hence \(\mathbb Z\) is not a characteristic subgroup.