Given a group \(G\) with identity element \(e\), a subgroup \(H\), and a normal subgroup \(N \trianglelefteq G\); then we say that \(G\) is the semi-direct product of \(N\) and \(H\) (written \(G=N \rtimes H\)) if \(G\) is the product of subgroups, \(G = NH\) where the subgroups have trivial intersection \(N \cap H= \{e\}\).
Semi-direct products of groups provide examples of non abelian groups. For example the dihedral group \(D_{2n}\) with \(2n\) elements is isomorphic to a semidirect product of the cyclic groups \(\mathbb Z_n\) and \(\mathbb Z_2\). \(D_{2n}\) is the group of isometries preserving a regular polygon \(X\) with \(n\) edges.
Let’see that the converse is not true and present a group that is not a semi-direct product.
The Hamilton’s quaternions group is not a semi-direct product
The Hamilton’s quaternions group \(\mathbb H_8\) is the group consisting of the symbols \(\pm 1, \pm i, \pm j, \pm k\) where\[
-1 = i^2 =j^2 = k^2 \text{ and } ij = k = -ji,jk = i = -kj, ki = j = -ik.\] One can prove that \(\mathbb H_8\) endowed with the product operation above is indeed a group having \(8\) elements where \(1\) is the identity element.
\(\mathbb H_8\) is not abelian as \(ij = k \neq -k = ji\).
Let’s prove that \(\mathbb H_8\) is not the semi-direct product of two subgroups. If that was the case, there would exist a normal subgroup \(N\) and a subgroup \(H\) such that \(G=N \rtimes H\).
- If \(\vert N \vert = 4\) then \(H = \{1,h\}\) where \(h\) is an element of order \(2\) in \(\mathbb H_8\). Therefore \(h=-1\) which is the only element of order \(2\). But \(-1 \in N\) as \(-1\) is the square of all elements in \(\mathbb H_8 \setminus \{\pm 1\}\). We get the contradiction \(N \cap H \neq \{1\}\).
- If \(\vert N \vert = 2\) then \(\vert H \vert = 4\) and \(H\) is also normal in \(G\). Noting \(N=\{1,n\}\) we have for \(h \in H\) \(h^{-1}nh=n\) and therefore \(nh=hn\). This proves that the product \(G=NH\) is direct. Also \(N\) is abelian as a cyclic group of order \(2\). \(H\) is also cyclic as all groups of order \(p^2\) with \(p\) prime are abelian. Finally \(G\) would be abelian, again a contradiction.
We can conclude that \(G\) is not a semi-direct product.

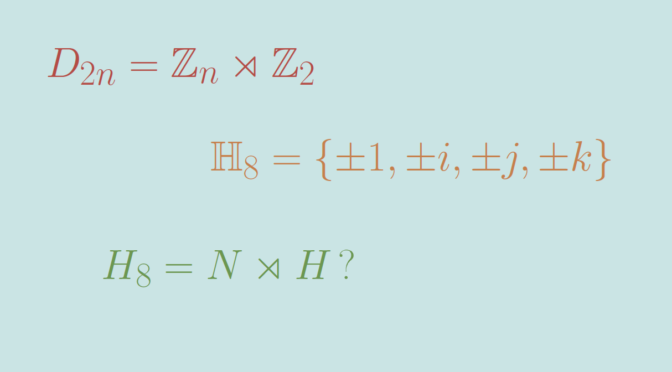
One thought on “A group that is not a semi-direct product”