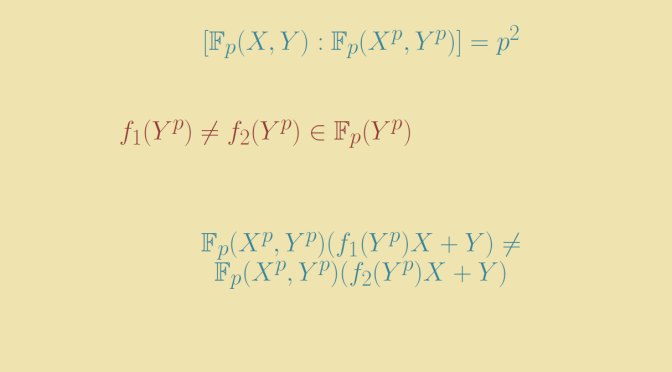Let’s consider \(K/k\) a finite field extension of degree \(n\). The following theorem holds.
Theorem: the following conditions are equivalent:
- The extension contains a primitive element.
- The number of intermediate fields between \(k\) and \(K\) is finite.
Our aim here is to describe a finite field extension having infinitely many subfields. Considering the theorem above, we have to look at an extension without a primitive element.
The extension \(\mathbb F_p(X,Y) / \mathbb F_p(X^p,Y^p)\) is finite
For \(p\) prime, \(\mathbb F_p\) denotes the finite field with \(p\) elements. \(\mathbb F_p(X,Y)\) is the algebraic fraction field of two variables over the field \(\mathbb F_p\). \(\mathbb F_p(X^p,Y^p)\) is the subfield of \(\mathbb F_p(X,Y)\) generated by the elements \(X^p,Y^p\).
The degree of \(\mathbb F_p(X,Y) / \mathbb F_p(X^p,Y^p)\) is equal to \(p^2\). To prove it, one can see on one side that \(\{X^iY^j \ : \ 0 \le i,j \le p-1\}\) are independent elements over \(\mathbb F_p(X^p,Y^p)\) which proves that \([\mathbb F_p(X,Y) : \mathbb F_p(X^p,Y^p)] \ge p^2\). On the other side a polynomial \(P(X,Y) \in \mathbb F_p(X,Y)\) can be written as a linear combination \[\sum_{0 \le i,j \le p-1} \lambda_{ij} X^iY^j\] where \(\lambda_{ij} \in \mathbb F_p[X^p,Y^p]\). And an element \(\frac{P}{Q} \in \mathbb F_p(X,Y)\) is equal to \(\frac{PQ^{p-1}}{Q^p}\) while \({Q^p}\) belongs to \(\mathbb F_p[X^p,Y^p]\) as can be proved using Frobenius endomorphism. Finally, \(\frac{P}{Q}\) can be written as linear combination \(\displaystyle \sum_{0 \le i,j \le p-1} \alpha_{ij} X^iY^j\) where \(\alpha_{ij} \in \mathbb F_p(X^p,Y^p)\) and we can conclude to \([\mathbb F_p(X,Y) : \mathbb F_p(X^p,Y^p)] = p^2\).
The extension \(\mathbb F_p(X,Y) / \mathbb F_p(X^p,Y^p)\) is not simple
For \(\theta \in \mathbb F_p(X,Y)\) we have \(\theta^p \in \mathbb F_p(X^p,Y^p)\) using again Frobenius endomorphism. Hence \([\mathbb F_p(X^p,Y^p)(\theta) : \mathbb F_p(X^p,Y^p)] \le p\) proving that \(\mathbb F_p(X,Y) / \mathbb F_p(X^p,Y^p)\) cannot have a generating element.
The theorem above allows us to conclude that \(\mathbb F_p(X,Y) / \mathbb F_p(X^p,Y^p)\) has infinitely many subfields.
Infinitely many subfields of \(\mathbb F_p(X,Y) / \mathbb F_p(X^p,Y^p)\)
For \(f(Y^p) \in \mathbb F_p(Y^p)\), the field: \[K=\mathbb F_p(X^p,Y^p)(f(Y^p)X+Y)\] is a nontrivial extension of \(\mathbb F_p(X^p,Y^p)\) and we can get that way infinitely many subfields between \(\mathbb F_p(X^p,Y^p)\) and \(\mathbb F_p(X,Y)\). Because for \(f_1(Y^p) \neq f_2(Y^p) \in \mathbb F_p(Y^p)\) if \(\mathbb F_p(X^p,Y^p)(r)=\mathbb F_p(X^p,Y^p)(s)\) with \(r=f_1(Y^p)X+Y\) and \(s=f_2(Y^p)X+Y\), we get \(X = (f_1(Y^p) – f_2(Y^p))^{-1}(r-s) \in \mathbb F_p(X^p,Y^p)(r)\), then \(Y \in \mathbb F_p(X^p,Y^p)(r)\) and \(\mathbb F_p(X,Y)\) would be finitely generated by \(r\). Hence for \(f_1 \neq f_2\) the extensions \(\mathbb F_p(X^p,Y^p)(f_1(Y^p)X+Y)\) and \(\mathbb F_p(X^p,Y^p)(f_2(Y^p)X+Y)\) are different.