A function \(f\) defined on \(\mathbb R\) into \(\mathbb R\) is said to be additive if and only if for all \(x, y \in \mathbb R\)
\[f(x+y) = f(x) + f(y).\] If \(f\) is supposed to be continuous at zero, \(f\) must have the form \(f(x)=cx\) where \(c=f(1)\). This can be shown using following steps:
- \(f(0) = 0\) as \(f(0) = f(0+0)= f(0)+f(0)\).
- For \(q \in \mathbb N\) \(f(1)=f(q \cdot \frac{1}{q})=q f(\frac{1}{q})\). Hence \(f(\frac{1}{q}) = \frac{f(1)}{q}\). Then for \(p,q \in \mathbb N\), \(f(\frac{p}{q}) = p f(\frac{1}{q})= f(1) \frac{p}{q}\).
- As \(f(-x) = -f(x)\) for all \(x \in\mathbb R\), we get that for all rational number \(\frac{p}{q} \in \mathbb Q\), \(f(\frac{p}{q})=f(1)\frac{p}{q}\).
- The equality \(f(x+y) = f(x) + f(y)\) implies that \(f\) is continuous on \(\mathbb R\) if it is continuous at \(0\).
- We can finally conclude to \(f(x)=cx\) for all real \(x \in \mathbb R\) as the rational numbers are dense in \(\mathbb R\).
We’ll use a Hamel basis to construct a discontinuous linear function. The set \(\mathbb R\) can be endowed with a vector space structure over \(\mathbb Q\) using the standard addition and the multiplication by a rational for the scalar multiplication.
Using the axiom of choice, one can find a (Hamel) basis \(\mathcal B = (b_i)_{i \in I}\) of \(\mathbb R\) over \(\mathbb Q\). That means that every real number \(x\) is a unique linear combination of elements of \(\mathcal B\): \[
x= q_1 b_{i_1} + \dots + q_n b_{i_n}\] with rational coefficients \(q_1, \dots, q_n\). The function \(f\) is then defined as \[
f(x) = q_1 + \dots + q_n.\] The linearity of \(f\) follows from its definition. \(f\) is not continuous as it only takes rational values which are not all equal. And one knows that the image of \(\mathbb R\) under a continuous map is an interval.

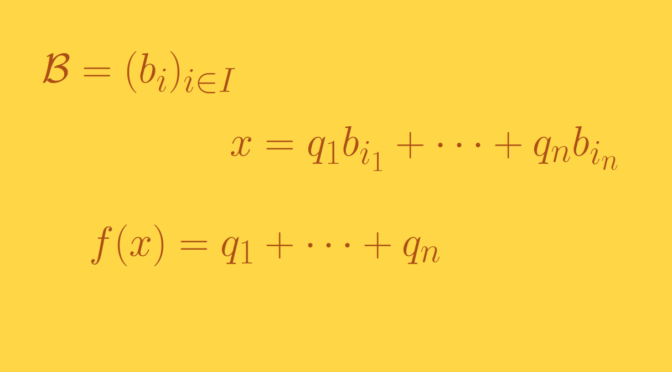
One thought on “A discontinuous additive map”