We build here a continuous function of one real variable whose derivative exists except at \(0\) and is bounded on \(\mathbb{R^*}\).

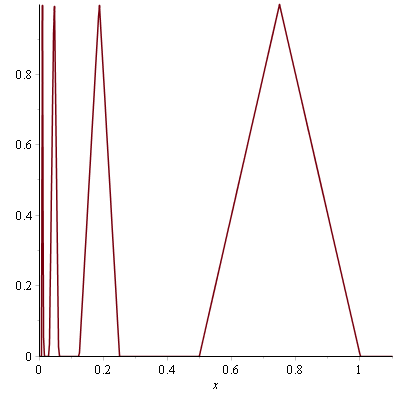
We start with the even and piecewise linear function \(g\) defined on \([0,+\infty)\) with following values:
\[g(x)=
\left\{
\begin{array}{ll}
0 & \mbox{if } x =0\\
0 & \mbox{if } x \in \{\frac{k}{4^n};(k,n) \in \{1,2,4\} \times \mathbb{N^*}\}\\
1 & \mbox{if } x \in \{\frac{3}{4^n};n \in \mathbb{N^*}\}\\
\end{array}
\right.
\]
The picture below gives an idea of the graph of \(g\) for positive values.

\(g\) is positive, bounded by \(1\) and continuous on \(\mathbb{R}\) except at \(0\). The support of \(g\) is included in the interval \([-1,1]\). Therefore \(g\) is integrable on every interval of \(\mathbb{R}\) (both Riemman-integrable and Lebesgue-integrable).

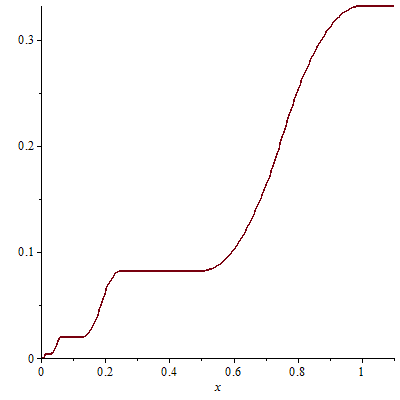
We then define \(\displaystyle f(x)=\int_0^x g(t) dt\). \(f\) has following properties:

• \(f\) is continuous on \(\mathbb{R}\) as defined as the integral of a function.
• For \(x \in \mathbb{R}^*\), \(f^\prime(x)=g(x)\). Which means that \(f\) is differentiable on \(\mathbb{R}^*\) with a bounded derivative as \(\vert f^\prime(x)\vert = \vert g(x) \vert \le 1\) for \(x \in \mathbb{R}^*\).
• \(f(0)=0\)

\(f\) graph looks like:

Let’s analyze deeper \(f\) for some real values. For \(n \ge 1\) integer we have:
\[\int^1_{\frac{1}{4^n}} g(t) dt = \sum_{k=1}^n \frac{1}{4^n} = \frac{1}{3}(1-\frac{1}{4^n})\] as this integral is the sum of the areas of triangles having a basis width equal to \(\frac{2}{4^k}\) and to \(1\) for their heights. In particular, as \(n \rightarrow +\infty\) we get \(\displaystyle f(1)=\int_0^1 g(t) dt = \frac{1}{3}\) and therefore:
\[f(\frac{1}{4^n})=\int_0^1 g(t) dt – \int^1_{\frac{1}{4^n}} g(t) dt = \frac{1}{3 \cdot 4^n} = f(\frac{2}{4^n})\] because \(g\) vanishes on all intervals \([\frac{1}{4^n},\frac{2}{4^n}]\).

For all \(n \in \mathbb{N^*}\) we have:
\[\frac{f(\frac{1}{4^n})-f(0)}{\frac{1}{4^n}-0}=\frac{1}{3} \mbox{ and } \frac{f(\frac{2}{4^n})-f(0)}{\frac{2}{4^n}-0}=\frac{1}{6}\]As \(\lim\limits_{n \rightarrow +\infty} \frac{1}{4^n} = \lim\limits_{n \rightarrow +\infty} \frac{2}{4^n} = 0\), we can conclude that \(f\) is not differentiable at \(0\).